
1. 기업의 이윤극대화 조건을 도출하시오.
2. 무차별곡선과 예산제약선의 개념을 설명하고 소득이 증가할 때 수요량이 어떻게 변하는지 설명하시오.
3. 완전경쟁시장의 단기균형에 대해 설명하시오.
4. 독점기업의 생산량과 가격이 어떻게 결정되는지 설명하시오.
5. 노동공급곡선을 도출하시오.
1. 기업의 이윤극대화 조건을 도출하시오.
이윤극대화 조건을 찾기 위해서는 우선 완전경쟁시장임을 상정해야 한다. 완전경쟁시장이란 1) 수많은 소비자와 생산자가 존재하여 시장의 왜곡이 없다. 2) 생산자가 공급하는 재화의 질적 차이가 없고 균형가격이 일정하다. 3) 소비자와 생산자는 필요한 모든 정보를 소유하고 있어 시장의 왜곡이 없다. 4) 기업은 각자의 판단에 따라 시장에 자유롭게 진출입할 수 있다.
이러한 상황에서 시장에서의 균형 생산량은 곧 개별기업의 이윤극대화 생산량이 될 수밖에 없다. 균형가격이 일정하므로 기업의 총수입은 생산량과 균형가격을 곱한 만큼이 되며 이것은 생산량의 증가에 따른 직선함수로 표현된다. 이때 기업의 이윤은 총수입에서 총비용을 제외한 값이므로 총비용의 변화에 영향을 받게 된다.
이제 총비용과 총수입의 그래프를 그려 기업의 이윤이 극대화되는 지점이 어딘지 찾아봐야 한다.

교재에 주어진 예시를 보면 고정비용은 20,000이며 생산량이 늘어날 때마다 한계비용은 증가한다. 따라서 생산량이 늘어날수록 총비용은 증가하게 되어 총비용함수의 그래프는 양의 볼록성을 띄게 된다. 앞서 총수입은 직선함수로 나타난다고 했고 총수입과 총비용의 차가 가장 큰 점이 이윤극대화점이 된다. 예시에서는 생산량이 10인 지점이 20,000으로 이윤이 가장 큰 지점이다.
이 그래프를 통해 찾아낼 수 있는 기하학적 의미는 바로 이 이윤극대화점에 총비용의 기울기와 총수입의 기울기가 같다는 것이다. 그리고 총수입의 기울기는 곧 한계수입이다.(한계수입은 일정함) 즉 한계수입 = 한계비용인 생산량에서 이윤이 극대화된다는 것을 알 수 있다.
만약 이러한 균형상태에서 기업이 생산량을 늘리면 총수입 증가량보다 총비용 증가량이 더 커서 이윤이 감소한다. 생산량을 감소시키면 총수입 감소량이 총비용 감소량보다 더 커서 역시 이윤이 감소한다. 따라서 기업은 이윤극대화 생산량 즉 균형생산량을 유지할 수밖에 없다.
2. 무차별곡선과 예산제약선의 개념을 설명하고 소득이 증가할 때 수요량이 어떻게 변하는지 설명하시오.
예산제약선이란 소비자가 재화를 소비하는 양상에 대한 함수라고 할 수 있다. 소비자의 소비능력은 예산의 제약을 받는다. 그 예산안에서 필요한 재화를 시장 안에서 자유롭게 소비하게 된다. 두 가지 재화만이 존재하는 시장에서 소비자가 한 가지 재화를 주어진 예산안에서 전부 구입한다면 다른 하나의 재화는 하나도 소비하지 못한다. 이것을 시장 가격과 예산, 소비량으로 그래프를 그려보면 아래와 같이 된다.
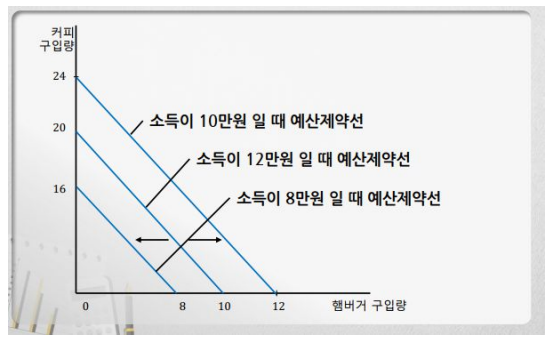
이 상태에서 소비자의 소득이 증가하는 등의 이유로 예산이 증가하거나 혹은 다른 이유로 예산이 감소하였다고 가정하면 그에 따른 예산제약선은 아래와 같이 이동할 것이다. 마치 수요 곡선의 이동과 유사하다.
이번에는 재화의 가격이 변화한다고 가정해 보자. 예산은 그대로인데 재화의 가격이 변하였으므로 예산제약선 역시 그에 따라 변화할 것이며 그래프를 그려보면 아래와 같다.

만약 여기서 커피 가격이 변동할 경우에는 수평 절편 즉 햄버거 구입량은 일정한 상태에서 예산제약선의 기울기만 변화하는 형태가 될 것이다.
예산제약선이 소비자에게 있어서의 수요곡선과 같은 개념으로 작용한다고 할 때 실제로 소비자가 어떻게 재화를 소비하는지는 소비자의 선호에 달려있다. 예산에 제약이 없는 상태에서 합리적인 소비자라면 자신에게 효용이 있는 만큼 최대한 많이 소비하기를 원한다. 그러나 현실에서는 주어진 예산의 제약이 있기에 예산제약선 상에서 상품의 소비가 이루어지게 된다.
소비자가 어떤 지점을 선택할 것인지에 대한 개념을 함수화 한 것이 무차별 곡선이다. 영어로는 Indifference Curve라 하는데 여기서 다름이 없는 대상은 바로 앞서 언급한 효용이라는 개념이다. 효용이란 어떤 재화나 서비스를 소비함으로써 소비자가 얻게 되는 이득, 행복감 등을 통칭한다. 우리는 지금 두 가지의 상품으로만 이루어진 단순한 가정을 하였으므로, 여기서는 커피와 햄버거를 각각 몇 개씩 묶어서 소비하였을 때 얼마만큼의 효용이 있는지를 계산하고 그 계산 값에서 효용 수준이 동일한 지점을 연결하면 그것이 무차별 곡선이 된다.

무차별 곡선을 그래프상에서 표현하면 위의 그림과 같이 된다. I2 곡선은 I1곡선보다 절대 효용값이 더 높은 곡선이다. 같은 곡선 상에서는 어느 지점이든 소비자 효용은 같다. 그리고 앞서 학습한 한계효용체감의 법칙 즉 한계효용 개념에 따라 무차별 곡선은 볼록한 형태를 가지게 된다.
3. 완전경쟁시장의 단기균형에 대해 설명하시오.
완전경쟁시장의 균형상태에서 기업이 생산량을 늘리면 총수입 증가량보다 총비용 증가량이 더 커서 이윤이 감소한다. 생산량을 감소시키면 총수입 감소량이 총비용 감소량보다 더 커서 역시 이윤이 감소한다. 따라서 기업은 이윤극대화 생산량 즉 균형생산량을 유지할 수밖에 없다.
개별 기업이 생산량을 조절할 수는 있지만 시장에 진입하거나 철수할 수는 없는 정도의 기간을 단기라고 정의했을 때 이러한 단기상태의 균형에 대해 생각해 볼 수 있다. 아래의 그림과 같이 시장가격이 평균비용보다 높은 점에서 형성되었을 때 기업은 초과이윤을 누리게 된다.
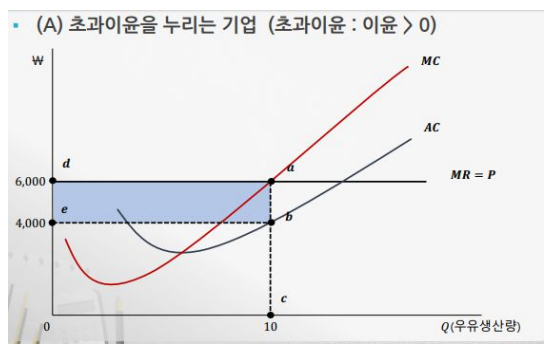
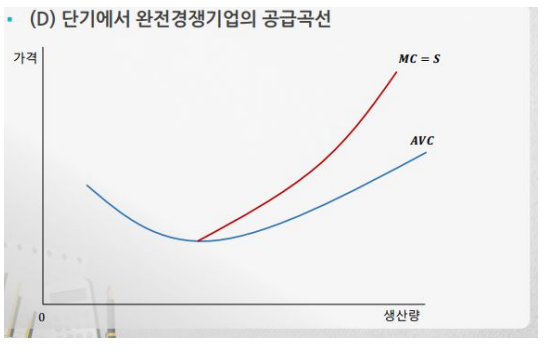
위의 그래프에서 시장가격이 한계비용(MC)의 그래프와 만나는 점에서 생산량이 결정된다. 앞서 이윤극대화 조건에 대해 알아보았는데, 시장가격이 평균비용곡선(AVC)의 최저점 미만이 된다면 오히려 손실이 발생한다. 이때는 이윤극대화 조건과 비슷하게 MR = MC인 점이 손실극소화 조건이 된다.
그리고 이 상황에서 기업이 생산을 중단해야 하는지 계속해야 하는지를 케이스 별로 정리해 볼 수 있다. 총비용에서 고정비용 전체가 매몰비용일 경우는 다음과 같이 대응할 수 있다.
1) 생산 중단 시 손실 = 고정비용(FC) = TC – VC
2) 생산 계속 시 손실 = TC - TR
1)이 2) 보다 작다면 생산을 계속할 필요가 없다. 즉 FC = TC – VC < TC – TR 일 경우, TR < VC가 되고, 양변을 Q로 나누면 P < AVC가 되어 시장가격이 AVC의 최저점보다 낮으면 생산을 계속할 필요가 없다.
고정비용이 일부 또는 전부 회수가 가능하다면 평균생산비용(AC)의 최저점보다 시장가격이 높다면 생산을 계속해야 손실을 최소화할 수 있다.
4. 독점기업의 생산량과 가격이 어떻게 결정되는지 설명하시오.
독점시장이란 생산자가 하나만 존재하여 그 생산자가 원하는 가격을 설정할 수 있는 시장을 말한다. 독점시장에서 생산자는 원하는 가격을 설정하여 그에 맞는 생산량만큼 재화를 생산할 수 있지만 결국은 그 상품에 대한 수요 곡선을 따라야 한다. 즉 생산량이 증가하면 시장 가격은 하락하고 생산량이 증가하면 시장가격은 상승한다.
따라서, 독점기업의 이윤극대화 조건도 한계수입(MR) = 한계비용(MC)인 지점이 된다. 교재에 제시된 예시에 따라 그래프를 그려보면 다음과 같다.

이때 이윤극대화 조건이 되는 지점은 A점이며 이때의 생산량은 Q*가 된다. 그리고 수요곡선을 통해 결정된 시장가격은 P*이다. 완전경쟁시장에서의 이윤 계산과 마찬가지로 이 경우에도 파란색 사각형의 면적이 독점기업의 이윤이 된다. 하지만 완전경쟁시장에서는 단기적으로는 초과이윤이 발생하나 새로운 공급자가 등장하는 장기 시장에서는 균형가격이 조정되어 초과이윤은 존재하지 않고 모든 기업이 정상이윤만을 취하게 된다. 독점시장에서는 독점기업의 초과이윤이 장기적으로도 유지된다는 점이 차이점이다.

이러한 차이점이 어떻게 그래프로 표현되는지 살펴보자. 독점시장의 생산량은 Q1이며 시장가격은 P1이다. 완전경쟁시장에서는 Q2가 되고 시장가격은 P2가 된다. 만약 독점 시장과 완전경쟁시장이 서로 다른 공간 혹은 국민국가에서 같은 상품 혹은 재화를 대상으로 발생했다고 가정한다면 독점 시장에서의 상품 가격이 더 높고 생산량이 더 낮을 것이다. 이것은 그만큼 소비자 편익, 사회전체의 편익이 감소한다는 것을 의미한다.
5. 노동공급곡선을 도출하시오.
노동공급곡선을 찾기 위해서는 앞서 배운 예산제약선과 무차별 곡선의 개념을 사용해야 한다. 노동자가 노동을 공급함으로써 임금을 받게 되고 나머지 시간은 여가로 활용한다. 임금과 여가를 두 가지 각기 다른 재화라고 생각하자.
노동자는 노동 시간에 해당하는 임금을 받게 되며 시간당 임금은 일정하다고 가정한다. 하루는 24시간으로 제약되어 있으므로 이에 해당하는 예산제약선을 다음과 같이 그릴 수 있다.
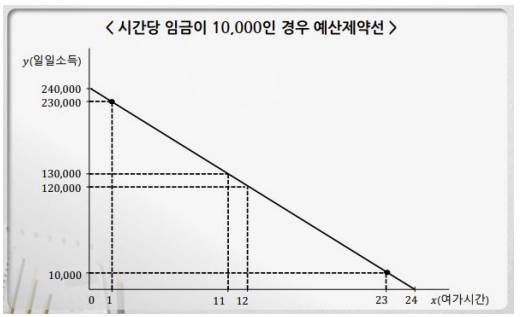
노동자는 이 예산제약선 상의 어떠한 지점도 선택 가능하며, 예산제약선을 벗어난 선택은 불가능하다. 어떤 지점을 선택할지는 앞서 정의한 노동자의 선호와 효용에 따른 무차별곡선을 그림으로써 특정할 수 있다.

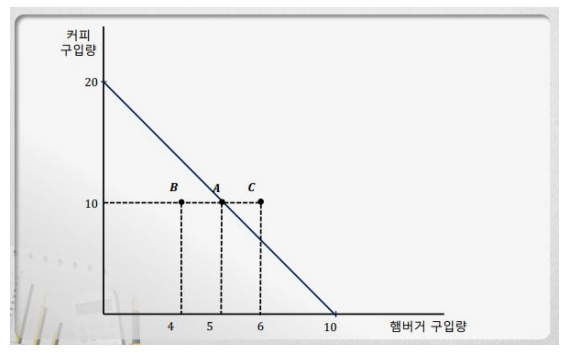
위 그림에 그려진 무차별 곡선에서 오른쪽에 위치한 것일수록 절대 효용값이 큰 곡선이다. 그리고 노동자는 예산제약선위의 지점만 선택이 가능하다고 하였으므로 위 그림에서는 r 곡선과 예산제약선이 만나는 A점이 노동공급점이 된다. 즉 위의 예시에서 노동자는 10시간 노동을 통한 10만 원의 임금 획득을 선택할 것이다. I1과 예산제약선이 만나는 B점과 B’ 점도 선택이 가능하나 노동자의 절대 효용값이 r 곡선에 비해 작기 때문에 선택되지 않는다고 본다.
노동공급선의 도출에 있어서는 시간당 임금의 변화가 하나의 변수로 작용할 수 있다. 시간당 임금이 변화하면 예산제약선의 수평절편은 일정한 상태에서 예산제약선의 기울기가 커지게 된다. 그러면 기존의 무차별 곡선 중 r 곡선이 아닌 I2 곡선과 예산제약선이 일치하는 지점이 생길 수 있다. 만약 C라는 점에서 I2곡선과 예산제약선이 만난다면 그 지점이 새로운 노동공급지점이 된다.
시간당 임금이 상승하거나 혹은 감소하는 변화에 대한 새로운 예산제약선을 쭉 도시하고 그에 따른 무차별 곡선 역시 차례대로 도시한다고 했을 때, 노동자가 노동시간을 늘릴 것인지 즉 여가시간을 많이 가져갈지 적게 가져갈지는 각기 다른 무차별 곡선의 형태에 달려있다. 이것은 노동자의 선호에 따라 다르게 나타나며 어떤 노동자는 여가시간을 늘리는 방향으로, 다른 노동자는 노동 시간을 늘리는 방향으로 움직이는 것도 충분히 가능하다.